摘要：中国箫笛的制作,自古以来都是凭借经验;即使是公式,也全都是经验公式,公式虽然具有可操作性,可不具有严密性。笛子制作和演奏技艺的发展,特别是现代音乐声学的发展,促使不少人对制作无法规范化的笛子进行规范的制作公式的探索,赵松庭先生的《横笛频率计算与应用》就是比较突出的实例。本文在肯定赵先生"公式"成就的同时,也指出公式的不足,意在引起物理学家的注意,促使"制笛公式"完善。

1956年，赵松庭先生随浙江省歌舞团在南京人民大会堂演出，一曲《早晨》使我倾倒。优美的旋律和以娴熟技巧所描绘的意境，真让人无法忘怀；当时笛子上所借用的唢呐“循环换气”法，更是让人称绝。这技巧不仅仅是笛子演奏技巧的一大突破，而且也是管乐器演奏技巧的一大突破因为这一技巧后来被长笛、萨克斯管等管乐器演奏所借鉴，解决了演奏长乐句运气不足的困难

笛子制作研究的科学化，目的旨在要求所制之笛有脆亮的音色、宽阔的音域和良好的音准。为了获得宽阔的音域，赵先生设计了排笛；为了力求所制之笛能有良好的音准，赵先生与其胞弟——复旦大学物理系教授赵松林先生，研究了“笛子制作计算公式”

中国的箫笛制作，自古以来是靠经验。1959年、轻工业部组织全国乐器试点组、总结北京、天津、苏州等地区的制笛经验，确定了"定调笛"制作尺寸。定调笛的制作尺寸和音准要求（依据国际标准音和十二平均律为音准标准）虽然有了明确的规定，但是并不等于音准就有了保证. 因为规定的尺寸，所据的仍然是经验

我国古代的箫笛制作，明确规定音孔位置和音高标准的，一件是公元274年荀勖所制定的“笛律"，并按照此"笛律"制作的"泰始笛"；另一件是初唐吕才制作的尺八、现代依据公式和具体音准制作的乃是20世纪30年代“今虞琴社”彭祉卿设计的“雅箫”。这三件乐器中就彭祉卿的“雅箫”来说，虽然讲述了各个音孔的定位方法，标准音为c1（黄钟箫）和升c1（大吕箫）、实际上所宗的仍然是经验，凭借的绝不是物理声学理论。有关“泰始笛”和“雅箫”制作的阐述比较繁琐、且与本文关系不大，故不作讨论，实际上“泰始笛"和"尺八"所述的乃是直笛，而不是横笛；"雅箫”当然是道地的箫了 尽管直笛（以及箫）同横笛的声学性质完全相同，音孔定位的方法也十分接近、但毕竟还是存在着不小的差异 中国有句老话："差之毫厘，失之千里"，直笛（包括箫）的制作公式即使十分科学，也绝对不能照搬到横笛上来 赵先生对横笛频率公式的推求，当属开拓性的研究

按照一般声学理论推导，笛子基音孔的频率公式应该是：

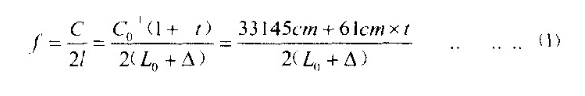
公式（1）中的f为频率，C为声波速度，l为筒音的气柱长，C0为一个标准大气压下摄氏零度时大气中的声波速度，L0为从吹孔至调音孔的管长，α为常数——温度每增高一摄氏度，声波速度增加61cm.t为温度，Δ为管口校正量，33145cm为摄氏零度时一个标准大气压下自由空间的声波速度。

频率公式（1），又可衍化成以下笛子制作的管长（从吹孔到调音孔）公式：

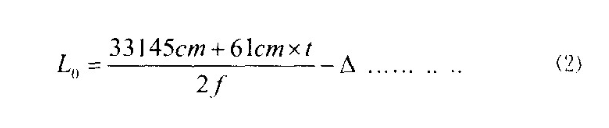
（1）式还可以衍化成音位（音孔位置）公式：

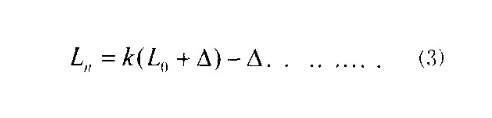
式中的k为生律法，在十二平均律则为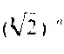，n为某音孔之音同基音孔之间的半音个数。

从表面上看，公式（3）简单、明了；实际上操作起来却很难。原因是公式中的声波速度为自由空间的速度，而笛的内径很小，管内的声波速度是否能等同于自由空间速度、这是需要验证的；如今却没有人测算验证。这是其一。其二是管口校正量△的值难以确定。国外曾有专家对笛管各音孔的频率进行过测算。因为某音孔的位置、同该音孔下方音孔的大小，以及下方音孔同该音孔之间的距离，对该音孔的频率都有影响，因此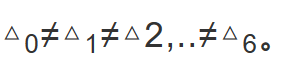。笔者也见过一些声学著作，将过去一些著名物理学家通过实验所取得的数据，归结出笛子的音位（音孔）公式，但是这些公式都过分繁难，根本就无法实际应用。

赵松庭先生推求笛子制作公式，是想努力将声波理论同实验所测得的数据结合起来，力图从理论上增强公式的可信度，同时更希望公式应用起来简便而具有可操作性。可惜赵先生没能更深入地研究下去，以至于让公式停留在有待进一步完善的阶段。但是赵先生的研究思路，无疑是具有开拓性的。

赵先生认为，笛子是"开管乐器"，因为笛子气柱的两端是与外界大气相接的，因此气柱的两端都应该进行校正。既然笛子的两端都与外界相接，它就该有两个校正量，即：管端校正量和末端校正量。

这儿需要说明一下，物理学家们早就将管乐器分成"开管"和"闭管"两类。由于"开管"、"闭管"问题，涉及形形色色的管乐器的形态及不同的声学性质，其复杂性非三言两语所能说清楚，因此就不作讨论。尽管如此，箫笛气柱振动时两端都需要进行校正，所应校正的情况，与赵先生所说是完全吻合的。

笛子制作的频率计算，两端需要进行校正，这两个校正量分别为末端校正量和管端校正量。也就是说，上述（1）式中的Δ，乃是末端校正量δ1同管端校正量δ2之和。当求得这两个量之后，在一定的温度下，给予笛子一定的频率，笛子的音位就应该可以求得。从道理上说，这是不错的. 但就实际的操作情况来说，要准确或比较准确地确定笛子的音孔位置，却存在着不少的困难。基于这个原因，笔者认为赵先生的公式就具有很大的不确定性。实际上本人一直认为赵先生所推算出的笛子制作公式，是一个有待进一步完善的公式。

所谓公式的完善，也就是公式中所选物理量得具备确定性和可靠性。现在让我们来看看公式要具备确定性所应有的准确的物理量。笛子所需要验证的物理量有三：一是笛管内的声波速度，二是末端校正量，三是管端校正量。首先让我们先来讨论一下笛管内的声波速度。

赵先生在计算频率公式时所选声波速度，为摄氏零度时一个标准大气压下的速度：331米/秒，温度每升高一摄氏度，声波速度增快0.6米。此处又有两个问题需要讨论：一是摄氏零度时的声波速度，一般为331.45米/秒，温度每增高一摄氏度声波速度增快0.61米。那么331米同331.45米之间，音高仅差2.35音分，若以440赫兹计算，频率仅差0.6赫兹，因此是可以忽略不计的。值得注意的是，这声波速度乃是大气中的自由空间的速度，而笛管的内径都比较小，一般都在2厘米左右，其间的声波速度恐怕不能简单地等于自由空间速度，这应该是需要验证的。声波速度的减缓，会使频率降低；当然，若减小管口校正量，同样可以弥补所降低的频率。这就需要对管口校正量进行确定性的研究。

关于末端校正量，赵先生认为“有两种不同形式"：末端的校正量是0.6r（r为半径），是不变的；另一种乃是各个音孔的校正量，此乃是一个变量。

尾端的校正量是否为0.6r？这0.6r的尾端校正量，那是指的标准管（两端管径相同），而末端没有调音孔的末端校正量。为此，笔者曾写过《瑞利的末端校正难适用于中国箫笛》，刊载在《星海音乐学院学报》1986年第1期上。再看看我们的笛子：末端有两个与音孔在同一平面上的助音孔，紧接着上端又有一对如"凤眼"一样的调音孔（这对孔才是末端）；何况笛子用竹制作，竹子的两端存在着相当大的管径差。因此，笛子的末端校正量就不能为0.6r。不仅如此，由于竹子两端管径差的不同，其校正量也就随着变化：管径差越大，末端校正量越大。

这末端校正量究竟应该是多少？缪天瑞先生在他的《律学》中说，"比利时声学家兼乐器研究家马容（Victor Mahillon 1841—1924）”研究，"管子长度+直径≈气柱长度"[1]。这个量，很可能就是有尾孔之管子的末端校正量。这个量用以下方法就可以求得。

用一支管子，管的上端开一吹孔，其下端于不同的部位开两对“凤眼”孔，检测分别掩没前后两对孔时吹奏频率，由于管端校正量没变，即可通过频率测得其校正量。这儿有个问题，即为什么不能求得准确的量？这可能是因为吹奏时气流没法绝对稳定，或者末尾之孔的孔径不标准的缘故。可惜缪天瑞先生引用苏联嘎尔布佐夫《音乐音响学》时，无法摘录全，因此无法知其详。

另一校正量则是音孔的管口校正量。赵先生计算这一校正量，不仅末端校正量欠合理，而日连分式也嫌繁琐,再就计算之结"果"来推算其"因",也足以证明此量不尽恰当以下就L赵先生《笛艺春秋》[2]中所载"常用竹笛计算数据"为例,看看其中之不足

例如"编号6的D调笛(曲笛)"的制作数据(第一行),吹孔至第二孔的长度为24.41cm,至第三孔为23.16cm,其间距为1.25cm;音孔的半径为0.5cm(直径为1cm),那么二孔之间的间隔(不是间距)仅为0.25cm,是否太靠近而致使食、中二指无法按孔?!

又如"计算实例三",赵先生已发现其中的不当,因此有一段补充说明:"此笛全按为a1(偏低),第二孔升C2不符,为老式的"骑墙音";其他各音也普遍低于标准,但在温度为25度以上时吹奏,则基本符合,"这段说明有不合理的地方.各音孔之间的音程不等,同整体音高的偏高或偏低是两回事,虽然同样是音不准,但是实际的情形却大不一样,整体音偏高或偏低,温度适当时其音高自然会得到矫正;但第二孔的"骑墙音"决不会因为气温的改变而使音程改变

这儿又产生了一个新问题,为什么实例二没产生整体音偏高或偏低,管径增大以后就产生了整体音偏低的问题"实际上看来答案也并不难寻,这只能证明笛管中的声波速度,不能简单地等同于大气中的声波速度:由于笛子的管径偏小,粘滞阻尼大于大气,且笛管越细.阻尼越大在这种情形下,我们若找到管径的变化与阻尼变化之间的关系.岂不就解决了问题?

再如"计算实例四",赵先生又加了个补充说明:"在实际的应用中,还要注意到手指的生理条件,例如上例,第二孔(24.6cm)到第三孔( 23.39cm)之间,由于是半音,因此距离较密(实际两孔的间隔0.21cm),手指按起来不太舒服解决这个问题,可用音孔大小不同的办法,比如说:将第二孔放大.那么就可以使第一孔和第二孔之间的距离缩短。将第三孔缩小一些,就可使第二孔第三孔之间的距离放宽一些。"（以上括号内数字为笔者所加）第二、三孔之间如此狭小的间隔，仅靠收小第三孔、增扩第二孔的孔径是不行的；何况这将造成音不准。

以上所分析的乃是末端校正量，以下再来讨论一下管端校正量.

关于管端校正量，赵先生归结为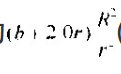（b为管壁厚度，R为管径，r为吹孔的平均直径）赵先生说：“实验表明，这个表达式，比较符合实际"。可惜赵先生已经作古，其实验的过程已不得而知，更不知赵先生的高足中是否有人留意此道。当然，赵松龄先生是重要的参与者，但他毕竟不是演奏家，恐怕即使问及也未必能得真髓

在求管端校正量时，赵先生将管径大小、管壁厚薄和吹孔大小都考虑进去，这无疑比前人的研究前进了一大进步.但是，根据自己制作、演奏和笛律理论的推求，认定赵先生所取得的这一数据同样还有待于完善。理由是，赵先生所求得的数据是静态的，管端校正量应该是动态的 其动态具体表现为，当各人演奏方法和运气情况不同时，音律情况（包括音高和音准）也就完全不相同。其具体的表现是，同一支笛子，演奏方法不同，其绝对音高和音准情况可以存在很大差异笛子已经制成，各个音孔的位置已经固定，管口校正量也同样稳定，何以会存在绝对音高和相对音高的差异呢？答案只有一个，已经制成的笛子，演奏时还有一个量在变动，那就是管端校正量！

笛子上还有一个问题，不知有人注意了没有、即：吹奏时笛子的任意一孔的音高，都比它所固有的音高要低100音分以上！这是什么缘故？这就是吹奏口唇靠近吹孔时，已增添了管端校正量，从而使频率降低

参考文献.

[1]缪天瑞、律学[M]人民音乐出版社，1983.1996、1999·10-11

[2]赵松庭.笛艺春秋[M].浙江人民出版社，1985，（3）