横笛的频率计算与应用-华音网

横笛的频率计算与应用

赵松庭华音网 2023-03-02

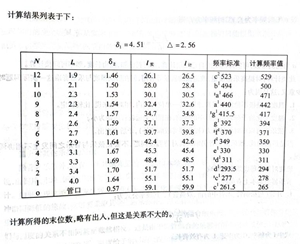
关于横笛频率的理论计算与实验开始于1961年，是我与同济大学教授赵松龄同志合作的。我经过两年的实验和探索，感到这理论分析是符合实际的，于是在1963年由赵松龄同志整理出《横笛频率理论计算》一文。近十年来，在原来工作的基础上，我们又做了大量的实验，积累了不少数据，并编写了数据表，希望能为一般笛子制造者提供一些方便。我们的探讨还有不完善之处（估计还有百分之二的误差），想通过本文引起有关方面关心，大家共同来探讨和实验，进一步解决横笛频率的计算和应用问题，乃至其他管乐器的计算和应用问题。

横笛是一个通称，它包括各种类型的中国竹笛、西洋长笛和短笛，以及乐器构造基本相同的各国民间笛子。我们的探讨以中国竹笛为主，也完全适用于长笛和短笛。对于其他类似的乐器，如箫等也基本适用。至于性质有同但又不完全相同的管乐器则只能在某些部分提供一些参考，如对单簧管、双簧管“音孔”的计算。

我国许多乐书、律书史籍中，记载了各种计算管律的资料。我们阅读这些史料时，感到前人为了解决这一问题已付出了许多劳动。但是，由于横笛的频率计算比较复杂，所以在理论上一直没有得到满意的解决办法。在生产实践中，主要靠经验，这种从实践中取得的经验是可贵的，我们重视它学习它、研究它，同时要结合声学原理把它提高到理论上来，再把这种理论付诸于实践，受实践的考验，发现问题，再进行修改，以求进一步的完善。

下面是我们探讨的初步结果。

一、“横笛”是开管

横笛究竟类似于“开管”呢，还是类似于“闭管”呢？这是一个带有根本性的问题。

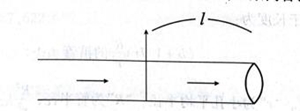
举中国笛子的基本构造为例：

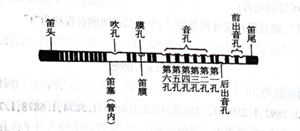
粗看起来，笛子一端闭塞，一端开口，直觉上容易认为它是"闭管"。以往许多学者就往往把它作“闭管”来分析研究。实际上，由于在吹孔处，管内空气柱已与大气接通，其振动方式与开管类似。因此，必须把它作"开管"来进行分析研究。下面的事实也可以证明横笛是"开管"而不是"闭管"。

闭管频率公式为：

开管频率公式为：

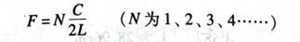
（式中"F"为频率，"C"为声速，"L"为有效管长）

假如笛子是“闭管”的话，那么在超吹时，频率将按1、3.5.7的奇数倍进，而吹不出高八度音。但事实上，笛子频率是按1.2.3.4的倍数进行的。例如：最低音为440，则用力吹时，为880，接着再用力吹时为1320，再用力吹则为1760，与“开管”情况相符。

假如笛子是"闭管"的话，那么从吹孔中心到笛塞之间的一段空隙的大小，对频率的高低有很大影响，距离1~3cm的变化，就可使频率升高或降低半个音甚至一个音左右。但事实上，这段空隙的大小，对笛子的音高（特别是低音）影响不大，距离1~3cm的变化，只能使频率升高或降低百分之一左右。这也与开管的情况相符。

由上所述，可以肯定笛子类似于开管，其频率公式为：

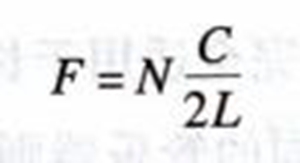
但是由于有其他因素的影响，在选定有效长度“L”时，要有相应的分析。

1.管的长度，需从与大气接通的吹孔中心量起，而不是从闭塞处或吹孔边缘量起。

2.管的实际长度“I”，与频率公式中的有效长度“L”，并不完全一致，须加以修正。

3.管的长度，量至第一个开放的音孔中心为止，但以下诸音孔的启闭情况，有相当大的影响。

4.吹孔和音孔的大小，管壁的厚度，唇部和面部的位置，温度的变化等等，都对频率起作用。

5.从吹孔中心到笛塞间的一段空隙（暂名为声囊），对频率的高低，有一定影响，但在计算低音（即基音）时，暂可略而不问。

二、确定频率标准与温度标准

目前，国际上采用平均律，为440赫兹。中国笛子是否采用平均律，是一个值得探讨的问题为了计算方便，应有一个统一的标准，我们在这里采用平均律和440的标准。

平均律的理论，可以简化为：

设主音频率为"1"，则其高八度音程为"2"，令十二音间的音程均为"t"

则：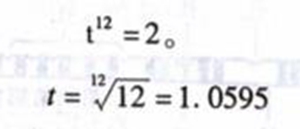

依次求得各音的比值为：

1.0595,1.1225,1.1892,1.2599,1.3348,1.4142,1.4983,1.5874,1.6878,1.7818,1.8877,2

设为440，以A为主音，求得十二音频率为：

440,466,494,523,554,587,622,659,698,740,784,830.5,880

基本公式中。“C”为声速，而声速与温度有关，我们取C=331＋0.6°C的算式。

另外，为了计算方便和切合实际需要起见，温度的标准取15℃。即声速=331＋0.6×15=349米/秒。

三、求出各音的有效管长“L”

用以上标准，代人基本公式分别求得各音的有效管长为：

高八度音乘二分之一，低八度音乘“2”。

（计算单位，统一用厘米“cm”。小数点以下，保留2位。）

四、管长修正数的计算方法

基本公式中，“L”为有效管长。

设实际管长为“l”，则L=1＋管长修正数。

管长修正数在吹端，是固定不变的，在出气端，则有两种不同形式：

1.以管的全部长度振动发声，出气的地方，在管口处。

2.以横开的音孔，缩短管长。其振动方式比较复杂，除吹孔下第一个开放的音孔能决定频率外，其他音孔的开放和闭合，也都对频率起着大小不同的作用。

第一种形式：

L=实际管长＋吹气端修正＋管口修正。

管口修正，已有理论和实验证明为：

管口修正=0.6R（R为管半径。）

第一种形式，我们写成为：

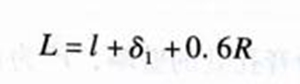
第二种形式：

L=实际管长＋吹气端修正＋出气端修正。

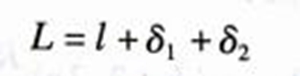
从以上分析中可以看出，我们需要解决的问题，实际上只有两个修正数，即和。

的求法

分析吹孔的声学特性，得出吹气端的修正数，在理论分析上，有相当大的困难；但是如果引入适当的简化假定，就可以根据声学理论，求出切合实用的表达式。

假定管壁上的小孔与平板上的小孔性质一样（实际上管壁为圆柱面，而并非平面，并不完全一样），那么，小孔的作用相当于长度为：

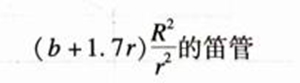
“式中“b”为管壁厚度。“r”为小孔平均半径。“R”为管半径，是折合成管长而引入的因子。以上述假定为基础，并假定吹奏时面部与唇部的影响，相当于在吹孔边上，竖立一垂直面，则可以求得吹孔的折合管长为：

式中“b”为吹孔处的管壁厚度。“r”为吹孔的平均半径。实验表明，这个表达式，比较符合实际。

的求法

的计算，比较繁杂，这是因为：

1.笛子各个音孔的大小与吹孔不一样，有时，各个音孔之间的大小也不一样。

2.管壁的厚度有时也不一样，例如，长笛就在吹孔处垫高0.4cm左右，其他音孔旁，都竖立0. 2cm左右的镶边。

3. 出气的音孔，有时会有其他情况。如老式的中国笛子，在基音孔处横开二孔，再在基音孔的后面开二个辅助音孔，既不适用0.6R的修正式，与其他音孔的修正式又有所不同。

4.吹笛时按住若干孔，开放若干孔。以开一二三孔（从下向上数）为例，各个开放的音孔，以及基音孔（或管口）都在出气。因此，原则上各开放音孔以及基音孔（或管口）都对频率有影响。影响最显著，具有决定性意义的，当然是从吹孔往下数来开放着的第一孔，但以下诸孔的影响也绝不能忽视。

根据这些情况，需要逐个进行分析。

情况之一：

音孔出气时，没有面部和唇部的影响；假如开放音孔的手指离开音孔较远，其影响可以略而不计（手指离开音孔过近，就对频率有关，一般来说，这是演奏的技术问题）。那么，其计算式列为：

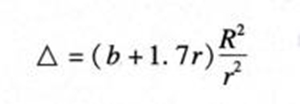
“△”为音孔处的折合管长，“b”为音孔处的壁厚，“r”为音孔的平均半径。

情况之二：

如果并列开两个小孔时，折合管长定为：

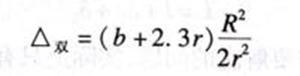
情况之三：

商品数量：

发音孔以下诸孔影响的分析：

只开管口时，其修正值即为0.6R。

开第一孔（从下向上数）时，出气有两条道路，一条沿管口，一条向音孔。

沿管口的折合长度为l+0.6R。

沿横孔的折合长度为：

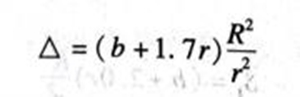
对于这两条并联的通路，其等效长度即为：

开多个孔时，可以归纳为：

设已知第N孔以下的修正数为，若再开放第N孔以上一孔，求相应的修正数。

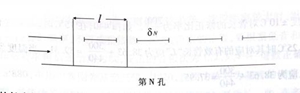
这时，沿管的长度折合为l+

沿横孔的折合长度仍为△

，则其等效长度为：

把以上1、2、3、点并在一起，即得连分式，

以开四孔为例：

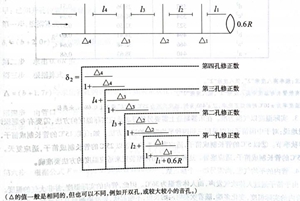
管长修正数的计算方法，基本上就是这些。

五、温度问题

温度与频率有关，在计算频率和实际应用中绝不能忽视温度的影响。由于温度是一个极不稳定的因素，因此它会在很大程度内妨碍乐器（特别是管乐器）的频率的稳定性。在管弦乐队中要解决温度与音准的关系问题，需要专题探讨，本文不准备详论，只就与横笛频率的计算与应用有关的方面提出几点看法：

1.在计算频率时，采用15℃的温度标准，求出各音的有效管长（如上所述）。

2.求出温度升高或降低时，对管长的修正比率。

从前述二公式中，即① ②C=331＋0.6℃

可以推出温度±10℃对管长的修正比率为。如：440，在15℃时，对应的有效管长“L”为38.63cm,温度为25℃时其对应的有效管长“L”应为38.63＋=39.31。当温度为5℃时，其对应的有效管长“L”，应为38.63-=37.95。

列表于下：

3.实际温度以气温为准。在乐器制造上需要另外寻求适应实际温度的方法，需要有专题探讨。一般地说：对于中国笛子可以采用三到四种平均温度的适应方法。如：①以15℃的管长制成笛子，适应春秋季节。②以5℃的管长制成笛子，适应寒冬季节。③以25℃的管长制成笛子，适应复天。④以35℃的管长制成笛子，适应盛暑。这种方法比用伸缩装置来适应温度的方法要准确。

4.管内的平均气温，尚需另加一个修正数。

由于笛子通过人体吹气发声，而人体常温为36℃。因此，管内的实际温度，并非大气的温度。同时，管内的实际温度，变化多端，随着吹奏时间的长短，不断起伏，要准确测量是困难的。据我们的实践经验，可以近似地列为：

管内平均温度=气温+（36℃-气温）

如：气温为15℃时，管内的平均温度，约为

15+(36-15)=22℃。

六、“笛塞”的处理

从吹孔中心到笛塞间的一段空隙，是能起“缓冲作用”的小容积。在一定的范围内，这段距离的大小，对频率没有很大影响。例如：距离在1~3cm间，频率变化在1%以内。发高音则影响增大。如原距离为1cm，假定发低音为“g²”，移动为2cm以后，低音仍为“g²”，高八度的音则偏低。移动到3cm后，低音比g²低1/4音左右，高音则偏低近半音。这段距离较大时，对高音的影响更显著，会使得低音与高音的频率，不再成整倍数。因此，笛塞的位置，要根据低音和高音之间是否为整倍数来定。在基音求得后逐渐用力吹，发出的音依次为1、2、3、4……倍数正确时（如基音为440，用力吹为880，再用力吹则为基音三倍1320，再用力吹则为基音的四倍1760），其距离即为正确。否则，就须放长或缩短。高音超过低音的整倍数时，要放长一些，高音不到低音的整倍数时，要缩短。一般这段距离的长度在0.5cm到1.6cm之间，也需随管径的粗细，略有改变。管径粗的应放宽一些，否则短一些。

七、计算方法和步骤

频率的计算与应用，有两个方面：一为已知开孔位置计算频率；另一为倒过来给一定频率值求得开孔位置。其他计算所需的因素包括：管的半径，吹孔和音孔的半径，壁厚以及温度都应为已知数（竹子的管半径和壁厚往往两端不一样，一般可以平均估计，精密一些，就应分开来量算）。

计算的方法和步骤一般如下：

也可用数值近似解法，即在连分式内，值取适当的数值代人，算出左方的值，将所得值再代人右方式内再算出左方值，这样反复代入几次，值不再变更，即为所求。例如：长笛（Flute）全按时为261.5，有效管长L=64.98，开第一孔为升277，有效管长为61.37，则△L=3.61。并已知△=2.56，故得第一孔的修正数：